Challenge Cup
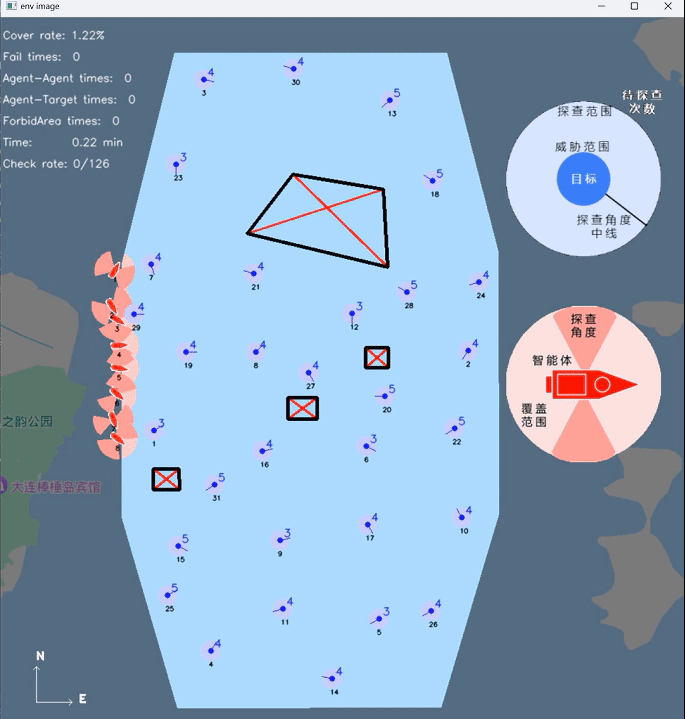 Photo by Jingyi HUANG
Photo by Jingyi HUANGOverall introduction
To inspire university students to actively participate in cutting-edge scientific research addressing critical national needs, the renowned science and technology competition, the “Challenge Cup,” introduced the special competition known as “Jie Bang Gua Shuai.” This year’s competition took place in Guizhou and featured a total of 21 topics, with over 2,000 projects in participation. We were proud to achieve the Grand Prize(特等奖) in this competition.

Faced with the challenge of information gathering in multiple unmanned marine regions, this project presents a multi-agent decision control model. We have devised multi-agent area coverage and task allocation algorithms and integrated trajectory planning algorithms based on Conflict-Based Search, along with velocity obstacle algorithms to ensure collision avoidance. An online optimization approach is employed to enhance overall coverage efficiency. Algorithm validation is conducted using platforms based on OpenCV and a self-developed simulation platform based on Cesium. Following multiple iterations of testing, our algorithm consistently achieves high-level performance, including an average area coverage rate of 99%, an average correct detection rate of 99%, and an average total time of 61 minutes.
Requirements
Duration: Apr. 2023 - Sept. 2023
Design a multi-agent decision control model for collision-free area information collection and target exploration within a convex polygonal target area:
- Complete coverage of the entire area;
- For each target, perform multiple scans at fixed angles;
- Avoid restricted zones and prevent collisions between agents.
In the end, we will deploy our model into the organizer’s simulation system, validating it using real ship dynamics. The final results will take into account the agent coverage ratio, the number of collision avoidance failures, and the overall simulation time.
Achievements
The following video showcases our final results (the video has been sped up):
Division
HAO Pengkun (Team leader)
Designed the framework, created the simulation environment, set coverage path planning algorithm, defined multi-agents’ decisions, coded OpenCV-based simulation, did the system integration.
WANG Yue
Set collaborative exploration and collaborative task allocation algorithm, did the system integration.
HUANG Jingyi
Used artificial potential fields algorithm for obstacle avoidance, coded A* algorithm, wrote practical functions such as to calculate the shortest distance between points and a convex hull, etc.
LIN Yuheng
Designed a multi-agent collision avoidance algorithm based on RVO (Reciprocal Velocity Obstacles)
Rest People
Built and debugged the cluster simulation platform – Potato. For more infomation about Potato, please click here.
Instructor : LI Xiaoduo, HAN Liang, REN Zhang
Our plan
Our algorithm consists of four algorithmic modules for executing subtasks and a cluster simulation platform for algorithm validation. The algorithmic modules for executing subtasks include the obstacle avoidance/collision avoidance module, the area coverage trajectory planning module, the target exploration module, and the task allocation module for multi-agent cooperation. The cluster simulation platform is built using Python, the OpenCV engine, and the Cesium engine.
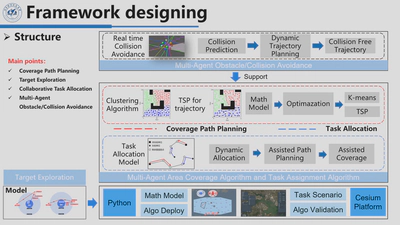
At the outset of algorithm execution, several pieces of information pertaining to the target area are initialized. Subsequently, the algorithm enters a loop to determine whether the task is completed. As long as the task remains incomplete, it executes a region-based coverage path planning algorithm while simultaneously employing a dynamic task allocation algorithm. The agent cluster collaboratively covers the area, thereby enhancing task efficiency. Throughout the entire task process, an obstacle avoidance/collision avoidance algorithm runs in real-time to ensure safety.
Obstacle Avoidance
Early stage - Artificial Potential Fields
In the initial stages of the project, the agent only needs to avoid targets. Therefore, we opted for the simplest obstacle avoidance control method, the artificial potential field method. Since the organizer did not provide a dynamic model for the agent, we used the simplest second-order model and PID control algorithm to ensure that it does not exceed the maximum speed provided by the organizer. At the planning level, all we need to do is design and output collision-free waypoints based on the information from the agent and the environment. For each agent, I need to first determine whether it needs obstacle avoidance. To do this, I have designed the need_doa method:
def need_doa(self):
# 判断是否需要进行智能体间避撞
list_doa_agent = []
for i in range(self.num_agents):
for j in range(i + 1, self.num_agents):
if self.agents[i].check_collision_agent(self.agents[j]):
list_doa_agent.append([i, j])
# 判断是否需要进行智能体和障碍物避障
list_doa_target = []
for i in range(self.num_agents):
for target_idx in range(self.num_targets):
distance = np.linalg.norm(
np.array([self.agents[i].position])
- np.array([self.targets[target_idx].coord])
)
if distance < self.obstacle_dist:
if self.list_doa_target_key[target_idx] == 0:
self.list_doa_target_key[target_idx] = 1
else:
list_doa_target.append([i, target_idx])
if len(list_doa_agent) > 0 or len(list_doa_target):
return True, list_doa_agent, list_doa_target
else:
return False, list_doa_agent, list_doa_target
After obtaining the list of agents that require obstacle avoidance and the targets, for each agent, we determine the next waypoint as the destination. We use the current position of the intelligent agent as the starting point and calculate the repulsive forces generated by the targets within 500m and the attractive force generated by the destination. We then calculate the next waypoint based on the resultant force of attraction and repulsion. To prevent the repulsive force from becoming excessively large when the agent is too close to a target, leading to waypoints being generated too far away or even outside the entire area, we set a constant value for the repulsive force within 50m.
Here K_rep represents the repulsion gain constant, D(q) signifies the distance between the agent and the target, and Q* denotes the critical distance used in the calculation of the repulsive force. We compute the repulsive force for all targets and aggregate them. Subsequently, we calculate the attractive force exerted by the goal on the agent. These repulsive and attractive force vectors are then combined to obtain the resultant force. Finally, we incorporate path points determined based on the resultant force into the navigation process.
Mid-term - Artificial Potential Fields with Avoiding Restricted Zones
Due to the initial simplicity of our scenario, we initially employed a basic artificial potential field method for obstacle avoidance. However, midway through the competition, the organizers introduced avoidance zones, requiring our agent to avoid these predefined convex polygonal areas while completing the area coverage task. To address this, we identified the closest point on the convex polygon to the agent and treated it as an obstacle. We then applied our existing obstacle avoidance framework to navigate around these zones without major modifications.
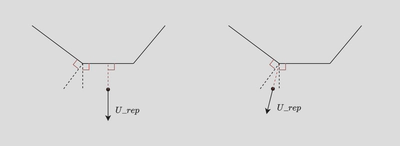
The method for finding the point on the avoidance zone closest to the agent is as follows:
def distance_point_to_line(point, line_start, line_end):
# 计算点到线段的最短距离
line_start = np.array(line_start)
line_end = np.array(line_end)
line_vec = line_end - line_start
point_vec = point - line_start
t = np.dot(point_vec, line_vec) / np.dot(line_vec, line_vec)
t = max(0, min(1, t)) # 确保点在线段上
closest_point = line_start + t * line_vec
distance = np.linalg.norm(point - closest_point)
return distance, closest_point
def shortest_distance_to_polygon(point, polygon_vertices):
min_distance = float('inf')
closest_point = None
# 遍历多边形的边
for i in range(len(polygon_vertices)):
start_point = polygon_vertices[i]
end_point = polygon_vertices[(i + 1) % len(polygon_vertices)]
distance, closest = distance_point_to_line(point, start_point, end_point)
# 如果找到更短的距离,更新最小距离和最近点的坐标
if distance < min_distance:
min_distance = distance
closest_point = closest
return min_distance, closest_point
However, through several rounds of testing, I have found that if both the target point and the intelligent agent’s position are located within the region enclosed by the perpendicular lines drawn from the two endpoints of a particular edge of the avoidance zone, a convergence point issue arises, preventing effective obstacle avoidance.
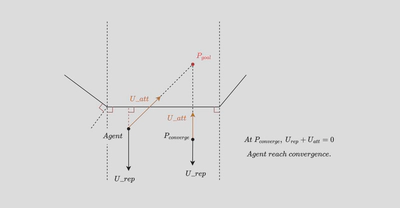
Late stage - A* algorithm
I realized that the artificial potential field method was inadequate for solving the current issue. Therefore, I started seeking a more general solution. I adopted the A* algorithm as the planning algorithm and computed real-time collision-free paths for the agent to reach the target point during simulation. The map had already been gridified for coverage path planning, allowing me to utilize the gridified map directly. The code is as follows:
#!/usr/bin/env python
# -*- encoding: utf-8 -*-
"""
Author: HUANG Jingyi
File: A_star.py
Date: 2023/9/8 11:28
Email: pierrehuang1998@gmail.com
Description:
"""
import heapq
import matplotlib.pyplot as plt
import json
import pyproj
import constants
import numpy as np
from Env import Env
class AStarPathPlanner:
def __init__(self, grid_map):
self.grid_map = grid_map
self.rows = len(grid_map)
self.cols = len(grid_map[0])
def heuristic(self, current, goal):
return np.sqrt((current[0] - goal[0])**2 + (current[1] - goal[1])**2)
def find_path(self, start, end):
start = tuple(start)
end = tuple(end)
if start == end:
return [[start[0], start[1]]]
open_list = [(0, start)]
came_from = {}
g_score = {cell: float('inf') for row in self.grid_map for cell in row}
g_score[start] = 0
f_score = {cell: float('inf') for row in self.grid_map for cell in row}
f_score[start] = self.heuristic(start, end)
while open_list:
_, current = heapq.heappop(open_list)
if current == end:
path = [current]
while current in came_from:
current = came_from[current]
path.append(current)
path.reverse()
path_list = []
for tpl in path:
path_list.append([tpl[0], tpl[1]])
# 将path修改为list类型
return path_list
add = [
(0, 1), (0, -1),
(1, 0), (-1, 0),
(1, 1), (1, -1),
(-1, 1), (-1, -1)
]
for dr, dc in add:
neighbor = (current[0] + dr, current[1] + dc)
if (
0 <= neighbor[0] < self.rows
and 0 <= neighbor[1] < self.cols
and self.grid_map[neighbor[0]][neighbor[1]] != 1
):
tentative_g_score = g_score[current] + 1
if tentative_g_score < g_score.get(neighbor, float('inf')):
came_from[neighbor] = current
g_score[neighbor] = tentative_g_score
f_score[neighbor] = (
tentative_g_score + self.heuristic(neighbor, end)
)
heapq.heappush(open_list, (f_score[neighbor], neighbor))
return []
I conducted tests using the test maps provided for this competition, and the results are as follows:
The whole frame
I have updated the logic for need_doa as follows: I now calculate the line segment formed by the current position of the agent and the target position. If this line segment does not intersect with the avoidance zone or the target, there is no need for obstacle avoidance. However, if it does intersect, I have implemented a choice between using A* or the artificial potential field method for obstacle avoidance based on whether the intersection occurs with the avoidance zone or the target. I have retained the artificial potential field method for two reasons: it offers relatively simple calculations, which can expedite simulation, and it helps minimize code modifications to prevent conflicts with the coverage and check tasks.